Hila Science Camp

Dome Math

Geodesic Domes

Dome builders call this type of dome a 2V Icosa Alternate. It is created by fitting 4 triangles inside each triangular surface of an icosahedron. What is an icosahedron?  An icosahedron is one of the 5 solids created by the ancient Greeks. Here are all five of them:

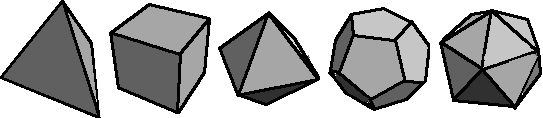
Can you name them? The last one on the right is an icosahedron, it has 20 triangular sides.

If you are really, really curious, follow this link to find out  how the triangles are fitted inside each triangle of an icosahedron - Icosahedron Domes Explained!
 

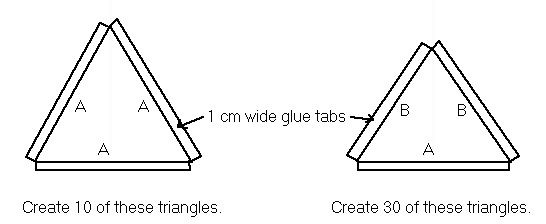
To create a dome similar to the one shown at top, you must create 40 triangles, 30 isosceles triangles and 10 equilateral triangles.
 

Let's design a dome!

Step 1:


Decide on the diameter of the dome you would like to create. Let's build a small model, 30 cm in diameter.
 

Step 2:


Determine the size of the triangles needed.  The triangles we are going to create, require glue tabs on their edges, they will look like this:

The 10 equilateral triangles have each side equal to a length "A". To determine "A" we use a number called a "Chord Factor".
The chord factor for "A" is 0.61803. To determine the length of "A" multiply the chord factor times the radius of the dome you are designing. Remember that radius = 1/2 of diameter. Our dome has a diameter of 30 cm and a radius of 15 cm.

A = radius of dome x 0.61803
A = 15 cm x 0.61803
A = 9.27045 cm
A=9.27 cm

The 30 isosceles triangles have one side "A" and two sides "B". We know "A" is 9.27 cm, to calculate "B" we use a different chord factor, the cord factor for "B" is  0.54653

B = radius of dome x 0.54653
B = 15 cm x 0.54653
B = 8.19795 cm
B = 8.20 cm

Step 3:

To construct this dome you must create triangular elements using the dimensions "A" and "B". Draw a 30 cm diameter circle on a solid cardboard base then follow the instructions for constructing the  50 cm dome.

You can create a dome of any size, just multiply radius times the chord factor.  Then follow the assembly sequence for the 50 cm dome.

Page created at:    Hila Science Camp: http://hilaroad.com